들어가기 앞서
모바일리더 코딩 테스트를 준비하면서 만난 나르시시즘 수는 굉장히 흥미로운 문제였다.
언젠가는 꼭 기록해야지 했는데 코딩 테스트를 본지 2주 후에 이렇게 기록하게 되었다.
근데 어떤 알고리즘으로 이 문제를 정의 내릴 수 있을지.. 잘 모르겠다.😵
나르시시즘 수?
Narcissistic number - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Integer expressible as the sum of the (number of digits)th power of each of its digits In number theory, a narcissistic number[1][2] (also known as a pluperfect digital invariant (PPDI
en.wikipedia.org
나르시시즘 수란 n의 모든 자리수에 k 제곱을 하고 더한 값이 n과 같은 경우 나르시시즘 수라고 한다. 혹은 자아도취 수.
우리나라에서 나르시시즘 수 혹은 자아도취 수로 구글에 검색하면 심리학에 대한 부분이 많이 나와서 영어로 검색 해야 한다.
문제
Arori | 당신의 지식
회원가입 조건이 맞는지 다시한번 확인해주새요
www.sysout.co.kr
(프로젝트로 진행했던 Arori에 문제를 작성해서 공부했다. 꽤나 잘 사용하는 중!)
어떤 자리 수 k가 주어졌을 때 각 자릿수의 k 제곱의 합이 원래 수가 되는 수를 자아도취 수라고 합니다. 예를 들어 153은 세 자리 자아도취 수입니다.
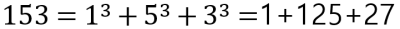
자연수 k가 매개변수로 주어질 때 k 자리 자아도취 수들을 배열에 오름차순으로 담아 return 하도록 solution 메소드를 작성하려 합니다.빈칸을 채워 전체 코드를 완성해주세요.
매개변수 설명
k가 solution 메소드의 매개변수로 주어집니다.
- k는 3 이상 6 이하인 자연수입니다.
return 값 설명
k 자리 자아도취 수를 오름차순으로 정렬한 뒤 배열에 담아 return 합니다.
예시
| k | return |
|---|---|
| 3 | [153, 370, 371, 407] |
예시 설명
- 153 = 1^3 + 5^3 + 3^3 = 1 + 125 + 27 = 153
- 370 = 3^3 + 7^3 + 0^3 = 27 + 343 + 0 = 370
- 371 = 3^3 + 7^3 + 1^1 = 27 + 343 + 1 = 371
- 407 = 4^3 + 0^3 + 7^3 = 64 + 0 + 343 = 407
풀이

설명
- 먼저 자연수
k는n의 자릿수의 제곱값인 것과 동시에n의 자릿수가 몇 개인지 알 수 있는 수이다. power()메소드는k만큼 반복하여 각 자리수의 자연수를 제곱값이 얼마인지 구해주는 메소드이다.
코드
package 모바일리더_코딩테스트_04;
import java.util.*;
public class question_06 {
public int power(int base, int exponent) {
int val = 1;
for (int i = 0; i < exponent; i++) {
val *= base;
}
return val;
}
public int[] solution(int k) {
// k를 통해 최대 범위를 구한다.
int range = power(10, k);
int[] answer = new int[range];
int count = 0;
// 나르시시즘 수는 range 범위 안에 존재한다.
for (int i = range / 10; i < range; i++) {
int current = i;
int cal = 0;
// i에 대한 각 자리수의 k제곱 값을 구한다.
// 각 자리수의 k제곱 값을 모두 합한 값 == cal 이다.
while(current != 0) {
cal += power(current % 10, k);
current /= 10;
}
// i에 대한 각 자리수의 k제곱 값을 모두 합한 값이
// i와 같다면 그 수는 나르시시즘 수이다.
if(cal == i) {
answer[count] = i;
count++;
}
}
int[] ret = new int[count];
for(int i = 0; i < count; i++) {
ret[i] = answer[i];
}
return ret;
}
// 아래는 테스트케이스 출력을 해보기 위한 main 메소드입니다.
public static void main(String[] args) {
question_06 sol = new question_06();
int k = 3
int[] ret = sol.solution(k);
// 실행] 버튼을 누르면 출력값을 볼 수 있습니다.
System.out.printf("solution 메소드의 반환 값은 ");
System.out.printf(Arrays.toString(ret));
System.out.printf(" 입니다.\n");
}
}'Algorithm' 카테고리의 다른 글
| Cos Pro 1급 | 비숍이 이동 가능한 칸 개수 찾기 (0) | 2020.12.10 |
|---|---|
| Cos Pro 1급 | 문자열 합성하기, 완전 탐색 (0) | 2020.12.10 |
| 백준 1322 | 비트 연산, X와 K (0) | 2020.11.25 |
| 백준 1158 | Queue, 요세푸스 문제 (0) | 2020.11.25 |
| 백준 10816 | 숫자 카드 2 (0) | 2020.11.07 |